דבר העורך, רון אהרוני
אם תכניסו \({101}\) יונים ל-\({100}\) תאים, לפחות שתיים מהן יצטרכו להצטופף באותו תא. זה אינו משפט מתמטי – זוהי עובדה טריוויאלית. אבל יש לה שימושים מתמטיים מעניינים. מאמר של אנה ליזהטוב (תבורך מנשים – לולא הייתה קיימת היה צריך להמציא אותה) מספר על העיקרון הזה.
מאמר של גדי אלכסנדרוביץ’ ושלי מספר על הכללה רב ממדית של העיקרון הזה. זהו משפט שגילה מתמטיקאי אנגלי בשם פרנק רמזי, גאון שמת בגיל צעיר מאוד.
יש גם השערת החודש, הפעם בתחום שנקרא “קומבינטוריקה אינסופית”.
וכמובן חידות ופתרונות.
חידוש נוסף: באדיבותם של מכון וייצמן והפקולטה למתמטיקה בטכניון, העלינו לאתר את כל הארכיון של “גליונות מתמטיקה”, האב הקדמון של “אתגר” ושל “נטגר”. יש שם הרבה פנינים. מומלץ!
אני רוצה לעודד אתכם להגיב עוד. תגובותיכם הן האדרנלין שמריץ אותנו. והן גם מועילות. למשל, בעקבות תגובותיכם הוספנו הערה מבהירה על ההוכחה שניתנה בגיליון הקודם למשפט פיתגורס.
עקרון שובך היונים
אנה ליזהטוב
עקרון שובך היונים
הנה משפט מתמטי שהוכחתו אינה מפורשת: בתל אביב יש שני אנשים שעל ראשיהם בדיוק אותו מספר שערות. אם תטענו שזה פשוט מדי, משום שיש שני אנשים קירחים לגמרי, אפשר לחזק את הטענה: יש שני אנשים לא קירחים לגמרי, עם אותו מספר של שערות.
ההוכחה מתבססת על עיקרון שנקרא “עקרון שובך היונים”: אם \(101\) יונים (או יותר) תיכנסנה ל-\(100\) תאים, יהיה תא שאליו ייכנסו לפחות שתי יונים. באופן כללי, אם מספר היונים גדול ממספר התאים, תצטרכנה שתי יונים (לפחות) להצטופף בתא אחד. הניסוח הכללי של המשפט הוא: כשמחלקים יותר מ-\(n\) עצמים ל-\(n\) סוגים (“תאים”), יהיו לפחות שניים מאותו סוג.
העיקרון הזה כה פשוט ומובן מאליו, עד שאפשר לתהות אם הוא יכול להועיל למישהו. למעשה זהו כלי שימושי ביותר, אפילו במתמטיקה גבוהה. סוד יופיו, וסוד הקושי בהוכחות המסתמכות עליו, אינו בעצם השימוש בו. הקושי הוא בבחירה נכונה של ה”תאים”, כלומר הסוגים שאליהם מחלקים את העצמים.
בואו נחזור עתה לשערם של תושבי תל אביב. עובדה היא שלאדם יש לכל היותר \(100,000\) שערות על ראשו. בתל אביב יש (נאמר) \(300,000\) אנשים, ואם מתעקשים על הנוסח של בני האדם הלא קירחים, מותר להניח שלפחות \(200,000\) מתוכם אינם קירחים. אם נחלק את תושבי תל אביב הלא קירחים לסוגים על פי מספר שערותיהם (כלומר בסוג הראשון אלה שיש להם שערה אחת על ראשם, בסוג השני אלה שיש להם \(2\) שערות על ראשם, וכו’), יתברר שיש יותר אנשים מאשר סוגים. לכן יהיו שני אנשים מאותו “סוג”, כלומר שני אנשים עם אותו מספר שערות.
קבוצות עצמאיות
קבוצת מספרים שלמים נקראת “עצמאית” (זהו שם שהמצאתי לצורך העניין) אם אין בה מספר אחד שמתחלק במספר אחר. למשל, הקבוצה \({3,5,6}\) אינה עצמאית, משום ש-\(6\) מתחלק ב-\(3\). הקבוצה \({3,4,5}\) היא עצמאית, משום ש-\(5\) אינו מתחלק ב-\(4\) או ב-\(3\), ו-\(4\) אינו מתחלק ב-\(3\).
כמה גדולה יכולה להיות קבוצה עצמאית של מספרים בין \(1\) ל-\(100\)?
כזכור, כלל יסוד בפתרון בעיות הוא לפתוח בדוגמאות פשוטות. במקרה זה כדאי להחליף תחילה את המספר \(100\) במספרים קטנים יותר, כאשר מותר, ואף רצוי, לקחת את הדבר לקיצוניות, כלומר לקחת מספרים קטנים ככל האפשר. נשאל אפוא תחילה מהו הגודל המקסימלי של קבוצה עצמאית של מספרים בין \(1\) ל-\(1\). כמובן: הקבוצה \({1}\) היא קבוצה עצמאית, ולכן הקבוצה העצמאית המקסימלית מכילה איבר אחד. ומה באשר למספרים בין \(1\) ל-\(2\)? הקבוצה \({1,2}\) אינה עצמאית (\(1\) מחלק את \(2\)), ולפיכך אפשר רק לקחת או את \({1}\), או את \({2}\) – גם במקרה זה הגודל המקסימלי של קבוצה עצמאית הוא \(1\). בין \(1\) ל-\(3\)? הקבוצה \({2,3}\) היא עצמאית, ומכילה שני איברים. בין \(1\) ל-\(4\): הקבוצה \({3,4}\) עצמאית, וכן \({2,3}\), וקל לראות שאין קבוצה עצמאית בת \(3\) איברים, אם כך גם במקרה זה התשובה היא \(2\). בואו נדלג עתה ל-\(10\): הקבוצה \({6,7,8,9,10}\) עצמאית, וכן הקבוצות \({5,6,7,8,9}\) ו-\({4,5,6,7,9}\). בכל אלה יש \(5\) איברים. קל למדי לבדוק שאין קבוצה עצמאית בגודל \(6\).
מן הדוגמאות שהובאו אפשר לנחש שאם \(n\) הוא מספר זוגי אז הגודל המקסימלי של קבוצה עצמאית של מספרים בין \(1\) ובין \(n\) הוא חצי מ-\(n\). אם \(n\) אי זוגי, כי אז הגודל המקסימלי הוא חצי מ-\(n+1\). למשל, קל למצוא קבוצה עצמאית בגודל \(50\) של מספרים בין \(1\) ו-\(100\): \({51,52,53,…,99,100}\), או גם \({49,50,51,52,…,99}\). אבל איך להוכיח שאין קבוצה עצמאית בת יותר מ-\(50\) איברים? הנה דרך יפה לכך. אנו רוצים להוכיח שקבוצה בת \(51\) איברים בהכרח אינה עצמאית. כלומר:
בקבוצה בת \(51\) מספרים בין \(1\) ל-\(100\) יש בהכרח שני מספרים שהאחד מהם מתחלק באחר.
ההוכחה נעזרת בעקרון שובך היונים. כרגיל, אקורד הסיום של ההוכחה, שהוא השימוש בעיקרון, לא יהיה קשה. הקושי הוא בשלב הראשון, של הגדרת תאי השובך. בין \(1\) ל-\(100\) יש \(50\) מספרים אי זוגיים. לכל מספר אי זוגי נגדיר “תא”, שהוא קבוצה של מספרים. תא זה יכיל את כפולות המספר האי זוגי האמור בחזקות של \(2\), כלומר במספרים\(1,2,4,8,16,…\). למשל, התא המתאים למספר האי זוגי \(3\) יכיל את המספרים: \(3*1=3\) , וכן את \(3*2=6\), את \(3*4=12\), את \(3*8=24\), ואת \(3*32=96\) (אנו לוקחים רק את הכפולות שאינן עוברות את \(100\), משום שאנו מחלקים רק את המספרים בין \(1\) ו-\(100\) לתאים). התא המתאים למספר האי זוגי \(25\) מכיל את \(25\), \(50\) ו-\(100\). התא המתאים ל-\(49\) מכיל רק שני מספרים – \(49\) עצמו, ו-\(98\) (הכפולה הבאה, ב-\(4\), כבר חורגת מן התחום). החל מן התא המתאים ל-\(51\), כל תא מכיל רק מספר אחד. התאים יהיו אפוא אלה:
\(1,2,4,8,16,32,64\) (אלה הן כפולות \(1\) בחזקות של \(2\));
\(3,6,12,24,48,96\) (כפולות \(3\) בחזקות של \(2\));
\(5,10,20,40,80\) (כפולות \(5\) בחזקות של \(2\));
\(7,14,28,56\) (כפולות \(7\) בחזקות של \(2\));
\(\dots\) (אני מדלג כאן על כפולות \(9,11,13,\dots\))
\(49,98\) (כפולות \(49\) בחזקות של \(2\));
\(51\)
\(53\)
\(\dots\)
\(99\)
נשים עתה לב לכך שכל מספר בין \(1\) ל-\(100\) מופיע באחד התאים. אראה זאת בדוגמה. באיזה תא יופיע למשל \(92\) ? חלקו את \(92\) ב-\(2\), ותקבלו \(46\); חלקו את \(46\) ב-\(2\), ותקבלו \(23\), שהוא מספר אי זוגי. אם כך \(92-23*2^2\), ולכן \(92\) יופיע בתא ה-\(23\), המכיל את כפולות \(23\) בחזקות של \(2\). אפשר לעשות כך עם כל מספר – למצות ממנו את חזקות \(2\) על ידי חלוקה נשנית ב-\(2\), עד שמגיעים למספר אי זוגי. הנה כי כן המספרים בין \(1\) ל-\(100\) מתחלקים ל-\(50\) תאים. על פי עקרון שובך היונים, אם ניקח קבוצה בת \(51\) מספרים יהיו בה שני מספרים שישתייכו לאותו תא. אבל שימו לב: אם שני מספרים שייכים לאותו תא, הגדול מהם מתחלק בקטן. למשל, המספרים \(12\) ו-\(96\) שייכים שניהם לתא של \(3\), משום ש:\(3*4=12\) ו-\(3*32=96\) . ואכן \(96\) מתחלק ב-\(12\) (משום ש-\(4\) מחלק את \(32\)). מכיוון שהראינו שבין \(51\) מספרים יש שניים שנמצאים באותו תא, הוכחנו לפיכך שבקבוצה של \(51\) מספרים בין \(1\) ל-\(100\) חייבים להיות שניים שהאחד מתחלק בחברו.
מספרים זרים
למתמטיקאי ההונגרי הגדול אֶרְדֶש סופַּר על ילד פלא, לָיוֹש פּושָה (Lajos Posa), שבגיל \(12\) כבר ידע מתמטיקה גבוהה. ארדש הזמין את פּושָה הצעיר למסעדה ואיתגר אותו: “הוכח לי שבקבוצה של \(51\) מספרים בין \(1\) ל-\(100\) יש שני מספרים זרים”, שפירושו מספרים שאין להם גורם משותף (כלומר שאין מספר, פרט ל-\(1\), המחלק את שניהם). פּושָה הרים את ראשו מקערת המרק ואמר: “בקבוצה של \(51\) מספרים בין \(1\) ל-\(100\) יש שני מספרים עוקבים” (כלומר נבדלים ב-\(1\)). כמובן, שני מספרים עוקבים הם זרים – אם למשל מספר מתחלק ב-\(3\), העוקב לו אינו מתחלק ב-\(3\).
גם כאן חבוי למעשה עקרון שובך היונים. הדרך הפשוטה ביותר להוכיח שבין \(51\) מספרים בין \(1\) ל-\(100\) יש שניים עוקבים היא לחלק את המספרים ל-\(50\) “תאים” של זוגות עוקבים: \({1,2},{3,4},{5,6},\dots,{99,100}\). בין \(51\) המספרים בקבוצה הנתונה יהיו שניים השייכים לאותו “תא”, שפירושו שהם יהיו עוקבים.
פּושָה פרש מן המחקר המתמטי בגיל צעיר. ארדש נהג לומר על כך ש”הוא מת”, אבל מבחינה אחרת הוא בהחלט חי. הוא הפך למחנך מתמטי שגידל דורות של תלמידים מצטיינים.
משפט רמזי
רון אהרוני וגדי אלכסנדרוביץ’
משפט 1 בין כל שישה אנשים קיימים שלושה שכולם חברים איש של רעהו, או שלושה שכולם לא חברים זה של זה.
(זהו “או” מתמטי – אפשר גם וגם).
נסו להוכיח לעצמכם את המשפט הזה – אפשר על ידי בדיקת מקרים, אבל יש גם דרך אלגנטית. כדאי לצייר את האנשים בתור נקודות, ויחס חברות בתור קטע שמחבר שתי נקודות. המשפט אומר אז שבציור שקיבלתם, שבלשון מתמטית נקרא גרף, יש משולש או שלוש נקודות שאין ביניהן קווים בכלל. דרך מקובלת אחרת היא לצייר קו בין כל זוג נקודות, ולצבוע אותו בצבע אחד (נאמר כחול) אם זוג האנשים המתאים חברים, ובצבע אחר, נאמר אדום, אם הם לא חברים. המשפט אומר אז שבצביעה כזו (שבה כמובן כל זוג מחובר באדום או בכחול) יש משולש כחול או משולש אדום.
ההבחנה הזאת היא מקרה פרטי של משפט שהוכח בשנות העשרים של המאה ה-\({20}\) על ידי מתמטיקאי אנגלי בשם רמזי \({(Frank~~Ramsey,~~ 1903-1930)}\). רמזי היה גאון רב תחומי, ומותו בגיל צעיר ממחלת כבד היה אובדן גדול למדע. הוא תרם ללוגיקה המתמטית ולתורת הכלכלה, ומצא גם זמן לעסוק בפילוסופיה. הוא אבי תורה שאומרת שמושג ה”אמת” מיותר – לומר שהמשפט “החתול שלי שחור” אמיתי לא אומר שום דבר נוסף על כך שהחתול שלי שחור. אפשר להסתדר בלי מושג ה”אמת”. לא צריך להתייחס ברצינות לתורה הזאת (להגיד שהמשפט החתול שלי שחור אמיתי מדבר על המשפט, ולא על החתול, וצריך לומר משהו גם על משפטים, לא רק על חתולים), אבל בואו נניח לפילוסופים לעסוק במלאכתם, ונחזור לענייננו – הצד המתמטי של מחקרו של רמזי.
כאמור רמזי עסק בלוגיקה מתמטית, שהוא תחום שמדבר על הקשר בין השפה המתמטית לבין האובייקטים המתמטיים שהיא מתארת, כמו מספרים, או גרפים, או צורות גיאומטריות. הוא הוכיח משפט מרכזי למדי, אבל שלא היה זוכה לתהילה, ולא היה מבטיח לרמזי מקום בפנתיאון המתמטי, לולא טענת עזר קטנה שהייתה בו. טענה שהיא הכללה של המשפט שלעיל, על שישה אנשים. ההכללה היא למספר כלשהו של אנשים, וליחסים שאינם דווקא בין שני אנשים, אלא גם בין שלושה או ארבעה, או מספר כלשהו. הטענה הזאת, ששימשה כ”למה” למשפט הגדול, הפכה במרוצת השנים לתורה מפותחת וענפה, שנקראת כיום “תורת רמזי”.
הפרק הבא בסיפור לא פחות מרתק. בסוף שנות השלושים החל לנבוט בבודפשט צמח מתמטי שעתיד היה לגדול לעץ רב ענפים. הגיבורים של הסיפור היו מתמטיקאי בשם קניג, ושלושה מתלמידיו – פאול ארדש, גיאורג סקרש (קראו בהונגרית – סגול מתחת לשלוש האותיות הראשונות) ואסתר קליין. קניג משך את תלמידיו לתחום שאז כמעט לא היה קיים, קומבינטוריקה. ב-\({1930}\), בעקבות שאלה שהציגה אסתר קליין, פרסמו ארדש וסקרש מאמר שהפך מאז לקלאסי, ודיבר על הכללות של עקרון שובך היונים – שעליו יש מאמר נוסף בגיליון הזה. בין השאר, את משפט רמזי ושימושים לו. שכן, כפי שנראה, משפט רמזי הוא הכללה רב ממדית של עקרון שובך היונים. ארדש וסקרש לא ידעו שהם מגלים מחדש משפט ידוע – הדבר התברר להם רק לאחר זמן.
סופו של הסיפור משמח – גיאורג סקרש ואסתר קליין התחתנו, הצליחו לברוח לסין לפני בוא הנאצים, בילו שם שש שנים, ואחר כך התגלגלו לאוסטרליה, שם מתו שניהם בשיבה טובה (כקוריוז, או יותר מכך כעדות לאהבתם, הם מתו בהפרש של שעה אחת).
בואו נחזור אל ששת האנשים שלנו, ונפתח בהערה: עם חמישה אנשים המשפט לא עובד. דרך נוחה היא להסתכל בציור. סדרו את \({5}\) הנקודות (אנשים) במעגל, וצבעו את הצלעות של המעגל באדום, ואת כל אלכסוניו בכחול. קל לראות שאין משולש אדום, וגם אין משולש כחול.
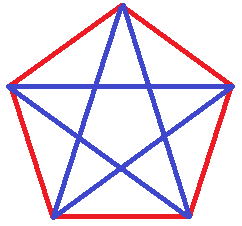
בצביעה הזאת של כל הקווים בין \({5}\) נקודות אין משולש אדום וגם אין משולש כחול. המסקנה היא ש- \({R(3,3)>5}\)
מדוע עם שישה אנשים זה כן עובד? בואו נעשה זאת שוב בגרף – “אדום” ו”כחול” הם מונחים נוחים לתפיסה. ניקח נקודה, נקרא לה א’. נניח תחילה שבין \({5}\) הנקודות האחרות יש \({3}\) שהיא מחוברת אליהן באדום, נאמר ב’,ג’ ו-ד’. אם יש בין ב’,ג’ ו-ד’ זוג שמחובר באדום הרי יחד עם א’ נוצר משולש אדום.
לכן מותר להניח שכל זוג נקודות בין ב’, ג’ ו-ג’ מחובר בקו בצבע כחול. אבל אז יש לנו משולש כחול – ושוב הצלחנו.
נימוק דומה עובד אם א’ מחוברת לשלוש נקודות בכחול.
ומה קורה אם מ-א’ יוצאים לכל היותר שני קווים אדומים ושני קווים כחולים? ובכן, זה לא ייתכן. במקרה כזה היו יוצאים מ-א’ יחד לכל היותר \({2+2=4}\) קווים – אבל יוצאים ממנה \({5}\) קווים!
בעצם, השתמשנו כאן בעקרון שובך היונים: אם צובעים \({5}\) עצמים באדום ובכחול, נמצא לפחות \({3}\) עצמים שצבועים באותו צבע.
התרגיל הבא בתור הוא להראות שאם יש \({9}\) אנשים, אז מובטח שתהיה שלישיית שונאים או רביעיית אוהבים (או לחילופין, תהיה שלישיית אוהבים או רביעיית שונאים – הסבירו לעצמכם למה זה לא אותו דבר כמו לומר שתהיה רביעיית אוהבים או רביעיית שונאים, מה שדורש כבר \({18}\) אנשים).
הנה התחלה של ההוכחה – שוב בלשון של גרף עם קווים צבועים באדום ובכחול. כאמור, צובעים את כל הקווים בין \({9}\) נקודות באדום ובכחול, ורוצים להראות שאו שיש משולש אדום, או שיש \({4}\) נקודות שכל \({6}\) הצלעות ביניהן צבועות בכחול.
ניקח בנקודה כלשהי. כמקרה ראשון, נסתכל במקרה שבו יוצאים מ-א’ (לפחות) \({6}\) קווים כחולים, כלומר יש \({6}\) נקודות שמחוברות ל-א’ בכחול. על פי משפט 1, בין \({6}\) הנקודות האלה אפשר למצוא משולש אדום או משולש כחול. אם יש משולש אדום – ניצחנו, הרי רצינו להראות יש משולש אדום. אם יש משולש כחול, אז יחד עם א’ מתקבלות \({4}\) נקודות שכולן מחוברות בכחול.
מקרה שני הוא שמ-א’ יוצאים \({4}\) קווים אדומים. אם בין ארבע הנקודות המחוברות ל-א’ באדום יש צלע אדומה – קיבלנו משולש אדום. אם כל הצלעות בין \({4}\) הנקודות האלה כחולות, קיבלנו \({4}\) נקודות שכל הצלעות ביניהן כחולות, ושוב ניצחנו.
פתרנו שני מקרים. האם הם מכסים את כל האפשרויות? לאו דווקא. מ-א’ יוצאים \({8}\) קווים. ייתכן בהחלט ש-\({3}\) מהם אדומים, ו-\({5}\) כחולים. אבל זוהי האפשרות היחידה שבה אף אחד מן המקרים האמורים לא מתקיים. וכאן באה הבחנה: זה חייב לקרות בכל נקודה. הרי א’ היא נקודה שרירותית. לכל נקודה, אם יוצאים ממנה \({4}\) קווים אדומים או \({6}\) קווים כחולים המשפט הוכח.
וזה כבר לא ייתכן. מדוע? אם מכל אחת מ-\({9}\) הנקודות יוצאים \({3}\) קווים אדומים, אז מספר הקצוות של קווים אדומים הוא \({9 \times 3}\), כלומר \({27}\). זה לא אפשרי בעליל: לכל קו (כמו לכל מקל) יש שני קצוות, ולכן מספר הקצוות של הקווים האדומים צריך להיות זוגי.
משפט רמזי הוא הכללה של שתי הטענות האלה.
משפט 2 לכל \({r}\) ו-\({s}\) קיים מספר \({N}\) שבהינתן \({N}\) אנשים, יש ביניהם \({r}\) אנשים שכולם חברים זה של זה, או קבוצה של \({s}\) אנשיעם שכולם אינם חברים זה של זה.
לאותו \({N}\) שבמשפט, אם נתונים יותר מ-\({N}\) אנשים ברור שהתנאי מתקיים (אומרים שהתנאי “מונוטוני ב-\({N}\)”) – הסבירו לעצמכם מדוע (למשל, מדוע משפט 1 נכון ל-\({7}\) אנשים). לכן מעניין לשאול על הערך הקטן ביותר של \({N}\) שמקיים את התנאי. הוא מסומן ב-\({R\left(r,s\right)}\) (עוד יותר ממשפט שקרוי על שמך, מכובד שיהיה סימון שנבחר על פי שמך!). בסימון הזה, משפט 1, בצירוף הדוגמה שהראתה ש-\({5}\) אנשים לא מספיקים, אומרים ש-\({R\left(3,3\right)=6}\).
תרגיל 1 הראו ש-\({R(3,4)=9}\).
(רמז: הנימוק שאמרנו לעיל מראה רק ש-\({R(3,4)\le 9}\). הראו ש-\({R(3,4)>8}\) – לשם כך דרושה דוגמה. של מה? ועוד רמז: בניות מוצלחות הן פעמים רבות סימטריות).
ההוכחה של משפט 2 היא באינדוקציה, ואינדוקציה קצת יותר מחוכמת מהרגיל במובן זה שהיא “דו ממדית”. כדי לחסוך במילים, נכתוב “אוהבים” במקום “חברים” ו”שונאים” במקום “לא חברים” (“לא חברים” יוצא קצת מסורבל).
ראשית שמים לב לכך שלכל \({r}\) ו-\({s}\) מתקיים \({R\left(1,s\right)=R\left(r,1\right)=1}\). מדוע? משום שקבוצה של אדם בודד היא תמיד קבוצה שכל חבריה גם אוהבים וגם שונאים (כל הקווים בתוכה כחולים, כי אין בכלל קווים, ממש כפי שכל הפילים שנמצאים בחדרי הם סגולים, כי אין פילים כאלה. וכמובן, כל הקווים בקבוצה של אדם אחד הם גם אדומים, כי אין קווים).
השלב הבא באינדוקציה הוא זה: אנחנו רוצים למצוא חסם עליון על \({R\left(r,s\right)}\) בהינתן שאנחנו כבר יודעים חסמים עליונים על \({R\left(r-1,s\right)}\) ו-\({R\left(r,s-1\right)}\). החסם העליון יהיה פשוט למדי – נוכיח שמתקיים \({R\left(r,s\right)\le R\left(r-1,s\right)+R\left(r,s-1\right)}\), וחסל.
אם כן, הבה ונתבונן על קבוצה בעלת \({R\left(r,s\right)}\) אנשים. ניקח איש אחד, נקרא לו א’, ונחלק את שאר האנשים לשתי קבוצות – חברי א’ ואויבי א’. מה שאנחנו רוצים לראות הוא שיש לא’ מספיק חברים או מספיק אויבים כדי להפעיל אחת מהנחות האינדוקציה.
אם לא’ יש לפחות \({R\left(r-1,s\right)}\) חברים, סיימנו – בקבוצה הזו או שיש \({s}\) אויבים (ואז סיימנו) או שיש בה \({r-1}\) חברים ואז יחד עם א’ נקבל קבוצה של \({r}\) חברים וסיימנו. בדומה, אם יש לו לפחות \({R\left(r,s-1\right)}\) אויבים סיימנו באותו האופן. למה לא ייתכן שאין לו לא מספיק חברים ולא מספיק אויבים?
כדי לא להתבלבל נכניס עוד כמה סימונים למשחק. \({A}\) יהיה מספר החברים של א’, \({B}\) יהיה מספר האויבים שלו, וראינו ש-
\(\displaystyle A+B+1=R\left(r-1,s\right)+R\left(r,s-1\right)\)
(הפלוס \({1}\) הוא כי גם את א’ סופרים). אז אם \({A<R\left(r-1,s\right)}\) וגם \({B<R\left(r,s-1\right)}\) זה אומר ש-\({A+B\le R\left(r-1,s\right)+R\left(r,s-1\right)-2}\), כלומר שלא ייתכן ש-\({A+B+1=R\left(r-1,s\right)+R\left(r,s-1\right)}\) (למי שעדיין לא רואה את זה, \({a<b}\) שקול לאמירה ש-\({a\le b-1}\) אם \({a,b}\) הם טבעיים; זו אבחנה מועילה מאוד לעתים).
זה מסיים את ההוכחה; עוד הרחבה לא מסובכת מטפלת במקרה יותר כללי, שבו זוג אנשים יכול להיות יותר מסתם חברים או אויבים, אלא יש \({s}\) סוגים שונים אפשריים של קשרים ביניהם – ושוב, אפשר להראות שלכל סדרת מספרים \({r_{1},r_{1},\dots,r_{s}}\) קיימת כמות אנשים שהחל ממנה, מובטח שעבור \({i}\) כלשהו יש קבוצה של \({r_{i}}\) אנשים שהקשרים ביניהם הם רק מסוג \({i}\).
המתמטיקאי תיאודור מוצקין (בנו של המנהיג הציוני שעל שמו קרויה קריית מוצקין -אגב, גם בנו של ז’בוטינסקי היה מתמטיקאי) ניסח זאת כך:
אין תוהו ובוהו מוחלט. בכל מבנה יהיו איים של סדר.
לסיום, הנה שאלה שנראית תמימה. ראינו ש-\({R\left(3,3\right)=6}\), כלומר שאם יש \({6}\) אנשים מובטחת לנו שלישיית חברים או שלישיית שונאים, וש-\({5}\) אנשים אינם מספיקים. אפשר להראות גם ש-\({R\left(4,4\right)=18}\). אם כן, מהו \({R\left(5,5\right)}\)?
נראה פשוט? כנראה לא כל כך. משפט רמזי אמנם נותן חסם עליון פשוט על \({R\left(5,5\right)}\), אבל אינו מצביע על הערך המדויק של המספר הזה. בדי עמל הצליחו המתמטיקאים להראות ש-\({43\le R\left(5,5\right)\le49}\), אבל זהו זה.
אתם עשויים לתהות – האם בימינו אי אפשר לתת את העבודה בידי מחשבים? ניקח את כל הצביעות האפשריות של הקווים בין\({43}\) נקודות, ונבדוק לכל אחת אם יש בה \({5}\) איברים שכל הקווים המחברים נקודות בתוכה הם מאותו צבע. ובכן, קל יותר לומר זאת מאשר לעשות. אפילו למחשב. יש \({903}\) קווים בין \({43}\) נקודות, ולכל קו יש שתי אפשרויות צביעה, ולכן מספר הצביעות האפשריות הוא \({\frac{43\cdot42}{2}=903}\). זהו מספר מאוד גדול. לשם השוואה, מספר האטומים ביקום מוערך ב-\({2^{250}}\). פירוש הדבר הוא שחיפוש ממצה אינו מעשי וגם לא יהיה מעשי בעתיד הנראה לעין. הכרחי יהיה לעשות הרבה עבודת הכנה מתמטית תיאורטית כדי שתהיה תקווה להריץ איזה חיפוש מחשב שגם יתן את התוצאה הנכונה. ואם נצליח, זו תהיה רק תחילת הדרך. מציאת \({R\left(6,6\right)}\) תהיה בהרבה סדרי גודל קשה יותר.
השערת החלוקה הלא ידידותית
רון אהרוני
הנה משפט קל וחביב. אני ממליץ לנסות להוכיח אותו עצמאית לפני שתקראו את ההוכחה.
משפט 1 – כל קבוצה של אנשים אפשר לחלק לשתי קבוצות, \({A}\) ו-\({B}\), כך שמספר החברים של כל אדם בקבוצה שאינו שייך אליה הוא לפחות כמספר החברים שלו בקבוצה שאליה הוא שייך.
</blockquote>
חלוקה כזאת נקראת “לא ידידותית”.
שימו לב שאין כאן כל הנחה על יחס החברות, פרט לסימטריה, כלומר שאם א’ חבר של ב’ אז ב’ חבר של א’. כל זוג של אנשים זכאי להיות חברים או לא חברים.
דוגמה: אם כולם חברים של כולם, חלקו את קבוצת האנשים בצורה שווה ככל האפשר (כלומר שהערך המחולט של ההפרש בין גדלי \({A}\) ו-\({B}\) יהיה לכל היותר \({1}\)).
הוכחת המשפט פשוטה מאוד: חלקו את קבוצת האנשים לשתי קבוצות, \({A}\) ו-\({B}\) כך שמספר יחסי החברות בין אנשים ב-\({A}\) ואנשים ב-\({B}\) מקסימלי (אם מציירים את יחס החברות כקו שמחבר את זוג החברים, בוחרים בחלוקה שבה מספר הקווים החוצים, אלה שעוברים מחלק לחלק, גדול ביותר.)
הטענה היא שתנאי ה”אי ידידותיות” (כל אחד חבר של יותר אנשים בקבוצה האחרת) נובע מן המקסימליות הזאת. נניח שלא. למשל, שיש אדם ב-\({A}\) שחבר של יותר אנשים ב-\({A}\) מאשר ב-\({B}\). העברתו של אדם כזה ל-\({B}\) מגדילה את מספר יחסי החברות חוצי הקבוצות, בסתירה להנחה שהמספר הזה הוא מקסימלי בחלוקה הנתונה.
והיכן כאן ההשערה? גם זה פשוט: המקרה האינסופי.
השערה – משפט 1 נכון גם כאשר יש אינסוף אנשים.
הדרישה במקרה האינסופי היא שאם מישהו חבר של מספר סופי \({n}\) של אנשים בצד שלו, הוא צריך להיות חבר של לפחות \({n}\) אנשים בצד האחר, ואם הוא חבר של אינסוף אנשים בצד שלו הוא גם חבר של אינסוף אנשים בצד האחר.
ההשערה הזאת, שנוסחה בידי מתמטיקאי אמריקני בשם \({Cowan}\), פתוחה מאז שנות ה-\({70}\) של המאה העשרים, כלומר יותר מ-\({40}\) שנים, ורבים וטובים ניסו בה את כוחם. אתם מוזמנים!
בינתיים מה שידוע הוא עובדה די פשוטה: שההשערה נכונה כאשר לכל אדם בקבוצה יש מספר סופי של חברים. נסו להוכיח זאת – אם תמצאו אנא שלחו פתרון. יש כאן חוכמה! אם יגיעו אלינו בקשות בעניין, נספר לכם את הפתרון בפעם הבאה.
חידות
דניאל לובזנס
דבר העורך: סוף סוף התחלתי לקבל פתרונות. חלקם מלאים ויפים. יש לתת את הדעת שרק כיוון מחשבה לפתרון, גם אם הוא נכון, לא מספיק. יש להסביר ולהוכיח בצורה הברורה לתלמיד תיכון את הטענות, ואם השאלה היא מספרית יש לחשב את התוצאה.
לחידות המוצגות בגיליון זה יפורסמו פתרונות בגיליון הבא. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 25.3.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה”ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.
חידה 1– עקומות על תפוחי אדמה?
האם תמיד ניתן לצייר על פני שני תפוחי אדמה שונים, עקומות סגורות כך שעקומה על תפוח אדמה אחד תהייה זהה לגמרי לעקומה על תפוח האדמה השני?

חידה 2– מה אורך החוט?
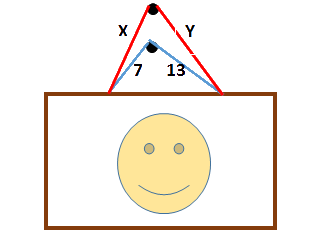
תולים תמונה בעזרת שני חוטים, המחוברים לצלע העליונה של המסגרת כמתואר בשרטוט. חוט אחד ארכו \(20\) ס”מ, קטע אחד שלו באורך \(7\) ס”מ והשני באורך \(13\) ס”מ, על מנת שהתמונה תהיה אופקית. החוט השני ארכו הכולל \(30\) ס”מ והוא מחובר למסגרת בדיוק באותן נקודות שבהן מחובר החוט הראשון, והמסמר שעליו הוא תלוי נמצא בדיוק מעל למסמר הראשון. מה אורך הקטעים \(X\) ו \(Y\)?
חידה 3– הזיקיות?
בגינה אחת נמצאות \(20\) זיקיות אדומות, \(18\) כחולות, ו \(16\) ירוקות. כששתי זיקיות בנות צבע שונה נפגשות, שתיהן מחליפות את צבען לצבע השלישי (למשל כשזיקית אדומה נפגשת עם ירוקה, שתיהן הופכות לכחולות. אם שתי זיקיות ירוקות נפגשות כלום לא משתנה). האם יתכן שאחרי מספר סופי של מפגשים בין הזיקיות לכל \(54\) הזיקיות יהיה אותו צבע? אם כן איזה צבע זה יהיה.
רמזים לחידות מגיליון פברואר 2015
חידה 1– סכומים של ספרות? – סכמו מ \(0\) עד \(999,999\) , נסו למצוא זוגות עם סכום ספרות קבוע.
חידה 2– מרכזי ריבועים על גבי מקבילית? – שרטטו את אלכסוני הרבועים, מצאו משולשים חופפים.
חידה 3– סכום של הופכיים? – קראו ב”נטגר” מינואר 2015 את מאמרה של אנה ליזהטוב “אינסוף מספרים שסכומם סופי”
פתרון החידות גיליון ינואר 2014
חידה 1– שנת 2015 בפתח
נוכיח את הטענה בנפרד ל \(N\) זוגי ול \(N\) אי-זוגי. נראה של \(1000^N-1\) קיים גורם שאין ל\(2015^N-1\) לכן אינו יכול לחלק אותו ללא שארית.
כאשר \(N\) זוגי \(N=2m\). \(1000^N-1=(1000000)^m-1=(1000000-1)(1000000^{m-1}+1000000^{m-2}+\dots+1)\)
\(1000000-1\) מתחלק ב\(13\), אבל \(2015^N-1\) אינו מתחלק ב\(13\) (כי \(155*13=2015\)) .
עבור \(N=2m+1\) . יש לתת את הדעת ש \(2015=9*224-1=9k-1\). בפיתוח הבינומי של \((9k-1)^{2m+1}\) כל האברים מתחלקים ב \(9\) פרט לאחרון שהוא \(-1\) לכן: \(2015^{2m+1}-1=9*l-1-1=9*l-2\), כלומר במקרה זה \(2015^N-1\) אינו מתחלק ב-\(9\) בעוד \(1000^N-1\) תמיד מתחלק ב\(9\).
חידה 2– מקלות הקטורת –
להלן פתרונו של משה דוידוביץ כלשונו:
נדליק את אחד המקלות משני קצותיו, ואת האחר מקצה אחד. כשהמקל הראשון יישרף לחלוטין, נדע שעברה חצי שעה. נדליק את המקל השני מקצהו האחר. כאשר הוא יישרף לחלוטין נדע שעברה רבע שעה נוספת ובסה”כ שלושת רבעי שעה כמבוקש.
חידה 3– קידוח הנפט –
נוכיח כי לכל מלבן \(ABCD\) וכל נקודה במרחב \(O\) מתקיים \(\overline{OA}^2+\overline{OC}^2=\overline{OB}^2+\overline{OD}^2\) (1).
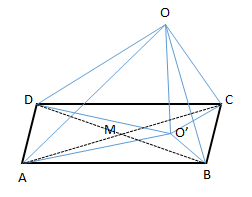
טענה: מספיק להוכיח את המשפט לגבי הנקודה \(O’\) שהיא ההיטל של הנקודה \(O\) על המישור \(ABCD\) .
הוכחת הטענה: עפ”י משפט פיתגורס מתקיימים השוויוניים:
\(\overline{OA}^2=\overline{O ‘A}^2+\overline{OO ‘}^2\)
\(\overline{OB}^2=\overline{O ‘B}^2+\overline{OO ‘}^2\)
\(\overline{OC}^2=\overline{O ‘C}^2+\overline{OO ‘}^2\)
\(\overline{OA}^2=\overline{O ‘A}^2+\overline{OO ‘}^2\)
לכן המשוואה: \(\overline{O ‘A}^2+\overline{O ‘C}^2=\overline{O ‘B}^2+\overline{O ‘D}^2\) (2) מתקיימת אם ורק אם מתקיימת המשוואה (1).
את (2) קל להוכיח ע”י שימוש במשפט פיתגורס במשולשים ישרי זווית הנוצרים מהעברת קוים המקבילים לצלעות המלבן דרך \(O’\).
בחרתי להציג הוכחה יותר אלגנטית לדעתי, נסתכל על נקודה \(O\) כלשהיא על גבי כדור החוסם את המלבן \(ABCD\) ומרכזו \(M\) מרכז המלבן (נקודת חיתוך אלכסוניו). המשולשים \(AOC\) ו \(BOD\) הם ישרי זווית כי הנקודה \(O\) בנויה על הקף מעגל שאלכסון המלבן הוא קוטרו.
לכן עפי משפט פיתגורס:
\(\overline{OA}^2+\overline{OC}^2=\overline{AC}^2\)
\(\overline{OB}^2+\overline{OD}^2=\overline{BD}^2\)
מאחר והאלכסונים במלבן הם בעלי אותו אורך: \(\overline{OA}^2+\overline{OC}^2=\overline{OB}^2+\overline{OD}^2\)
ובעזרת הטענה הקודמת: \(\overline{O ‘A}^2+\overline{O ‘C}^2=\overline{O ‘B}^2+\overline{O ‘D}^2\) .
יש לתת את הדעת שההוכחה נכונה לנקודה \(O’\) בתוך המלבן אבל בקלות ניתן להכלילה לנקודה \(O”\) מחוץ למלבן כפי שניתן להדגמה על ידי שני האיורים הבאים:
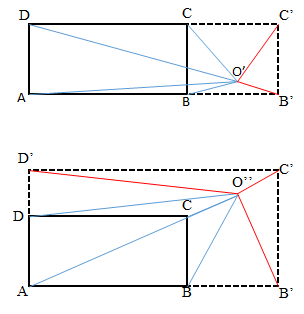
באיורים הנקודה \(O”\) מחוץ למלבן \(ABCD\), אבל בתוך מלבנים גדולים יותר (\(AB’C’D\) ו- \(AB’C’D’\)), עם אותם ארכי קטעים לקדקדים.
מכאן קל לחשב את המרחק המבוקש:
\(X=\sqrt{4700^2+3200^2-5200^2}=2300\)
שמות הפותרים נכונה את החידות מגיליון פברואר 2015
עומר שמחי, כתה י”ב אורט טבעון – חידה 2
תומר – חידה 1
משה דווידוביץ – חידה 2
אוהד שיינפלד –חידה 2